(Summary: I propose that we should use inequalities with asymptotic notation like big-
, big-
, little-
, little-
, and 
when they represent only an upper bound or only a lower bound. E.g., 
or 
or 
.)
Recall the big- asymptotic notation. E.g., for two functions 
, we write 
to mean that there is some universal constant 
such that 
. (Of course, there are many many variants of this. I tried here to choose a setting—functions whose domain is the positive integers and range is the positive reals—in which this notoriously ambiguous notation is least ambiguous. But, everything that I will say about big- notation below has exceptions. Indeed, any attempt to formally define how this notation is actually used in any reasonable amount of generality will quickly fail in the face of our collective notational creativity.) For example, 
and also 
, but 
and 
. As a more complicated and mildly interesting example, we have 
but 
. (Proving the latter fact requires a tiny bit of diophantine approximation.)
To greatly understate things, this notation is useful. But, a common complaint about it is that it is an abuse of the equals sign. (Deligne points out that the equals sign is actually abused quite frequently.) Indeed, it is a little disconcerting that we write an “equality” of the form when the left-hand side and the right-hand side don’t even seem to have the same type. (What even is the type of the right-hand side 
? The left-hand side is clearly a function of a variable 
. The right-hand side clearly is not a function of , since it makes no sense to ask what its value is at, say, 
.) And, it is quite worrisome that this use of the equals sign is not at all symmetric, since certainly does not imply that 
(and we would never write 
).
These problems are of course confusing for people when they first encounter the notation. But, they also lead to many little annoying issues in actual papers, where even brilliant computer scientists and mathematicians will frequently write silly things like “we prove a lower bound of 
on the running time of any algorithm for this problem.” This is presumably meant to suggest that the lower bound is good in that it is reasonably large (presumably that it grows quadratically with ) but when interpreted literally, this statement suggests that the authors have proven some unspecified lower bound 
satisfying . For example, a lower bound of 
on the running time of an algorithm is almost never impressive but certainly satisfies this. (In such cases, the authors usually mean to say “we prove a lower bound of 
.”)
Of course, this is really just pedantry, since in almost all such cases it is perfectly clear what the authors meant. But, (1) pedantry is good; (2) saying “what I wrote is technically wrong but the reader should be able to figure it out” is rarely good; and (3) in even slightly more complicated or less clear cases, this can and does lead to confusion or even bugs.
A commonly proposed resolution to this is to interpret as the set of all functions such that 
is bounded. Then, rather than writing , one should write 
. A lot of people like to point out that this is technically more accurate (see Wikipedia), and one occasionally sees such notation used in the wild. However, it is used quite rarely, in spite of the fact that people have been pointing out for decades that this is the “technically correct notation.” I won’t pretend to truly know how other people’s minds work, but I suspect that the reason that this notation has not caught on is simply because it does not match how we think about big-. I don’t think of as meaning “
is in the set of functions such that…”, but instead, I think of it as representing an upper bound on . (Of course, more-or-less any mathematical notation can be defined in terms of sets, and in many formal axiomatizations of mathematics, everything simply is a set. E.g., an overly formal interpretation of the notation 
is really saying that the ordered pair 
is contained in the set of ordered pairs defining the relation 
. But, we do not parse it that way in most situations. So, the fact that it is technically consistent to view the statement as placing in a set is not very interesting. The question is really whether it’s actually convenient to view the notation in this way.)
So, I propose that we use inequalities with big- notation in this context. For example, I propose that we write 
. To me, this simply represents exactly what is meant by the notation. Indeed, it is difficult for me to read 
and interpret it in any way other than the correct way. Specifically, it represents an asymptotic upper bound on in terms of 
. (Here and throughout, I am using blue to represent the notation that I am proposing and red to represent the more standard notation.)
In fact, I find that this notation is so intuitive that in my papers and courses, readers immediately know what it means without me even having to mention that I have switched from the more conventional to the variant . (This is why I view this as a quite “modest” proposal.) One can therefore simply start using it in ones work without any fanfare (or any apparent downside whatsoever)—and I suggest that you do so.
More generally, when asymptotic notation is used to represent an upper bound, we should write it as an upper bound. Anyway, that’s the high-level idea. I’ll now go into more detail, explaining how I think we should write more complicated expressions with asymptotic notation and how to use the same notation in the context of big-, little-, little-, big-
, and . To be clear, this idea is not novel, and one can already find it in many papers by many excellent authors. It seems that most authors mix inequalities and equalities rather freely in this context. (I asked ChatGPT to find early examples of this notation, and it found a 1953 paper by Tsuji, where he uses this notation in chains of inequalities. More generally, this notation is more often used in the literature in chains of inequalities and in other spots where inequalities might seem more natural than equalities.) I am merely advocating that we as a community try to use it consistently—in papers and in teaching.
Fancier use cases and choosing the direction of the inequality
Of course, big- notation gets used in fancier ways than simply writing things like 
. For example, one might wish to say that an event happens with probability that is at least 
for some constant 
, which many will write quite succinctly as 
. Now the big- has made its way all the way up to the exponent! And, because of the minus sign, this is actually a lower bound on using big- notation, whereas simpler uses of big- always yield upper bounds.
In this case, I naturally propose writing 
. This again makes it very clear what’s going on—we are giving a lower bound on .
One might have a more complicated expression such as 
or something, where it is quite easy to get confused about whether an upper bound or lower bound on is intended. (Yes, I know that this expression simplifies.) In these cases, using an inequality sign provides some help to the reader, as evidenced by how much easier it is (at least for me) to parse the expression 
. So, one does a real service for the reader by writing 
.
There are also examples where the traditional notation is actually formally ambiguous. This often occurs when big- is used around a lower-order term, such as in the expression 
. Here, it is not clear whether one simply means that 
for some constant 
, or if one means that 
for some constant 
. (A formal reading of the definition of big- would suggest the former, but I think authors typically mean the latter. Admittedly, some of the ambiguity here comes from the question of how big- interacts with functions taking negative values, which I am deliberately ignoring.) Here, the notation that I am proposing can help a bit, in that one can write 
in the first case while still writing 
in the second case. (Of course, unless this notation comes into very widespread use, one should not assume that the reader recognizes the distinction. One should often clarify in more than one way what one means in cases where the risk of ambiguity is great. When it doesn’t matter much—e.g., in an aside, or in a case where the weaker fact 
is all that’s needed but the stronger fact that is true—one can simply rely on this notation to suggest the correct interpretation without burdening the reader with much discussion.) In particular, notice that if one truly means that 
, then the use of the equals sign in the expression 
is actually justified, since we are in fact placing in an equivalence class in this case (whereas the notation does not place in any reasonable equivalence class). We will see more examples of this below
All of this means that authors who use this convention must be sure to carefully think about what specifically they mean when they write asymptotic notation. That is a good thing.
Cousins of big-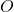
Big- also has its close cousins big-, little- and little-, and it is relatively straightforward to see how these notations should be modified.
- Big- 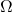the old way: One typically writes
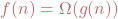if and only if there is some universal constant 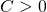such that 
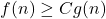. Equivalently, 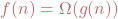if and only if .
My recommendation: As you might guess, I recommend instead writing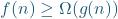
, to make clear that the big- 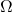notation is giving a lower bound. - Little- the old way: One typically writes
if and only if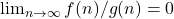 
.
My recommendation: I recommend instead writing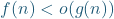
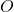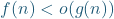. This makes clear both that the little- notation is giving an upper bound, and in my opinion the strict inequality does a good job of representing the distinction between big- and little-. In particular, means that 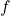is “asymptotically strictly smaller” than 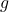, where the fact that this inequality is strict is justified formally by the fact that 
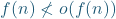. - Little- 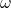the old way: One typically writes
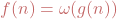if and only if 
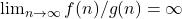. Equivalently, 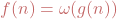if and only if 
.
My recommendation: As you might guess, I recommend instead writing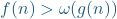
. - Big- 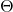the old way: One typically writes
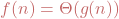if and only if 
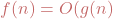AND .
My recommendation: Keep doing it the old way! When we write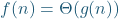
, we are in fact proving both an upper and lower bound on 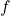and we are relating 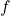and 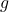according to an equivalence relation. So, in this case, the traditional notation is already great!
As before, in slightly more complicated expressions the inequality sign can flip. E.g., 
is a perfectly good lower bound in terms of little-, just like 
is a lower bound in terms of big- and 
is an upper bound in terms of little-. And, sometimes the specific choice of which (in)equality symbol to use can convey additional meaning that is not clear without it, like in the expression 
, where the inequality is meant to make clear that an upper bound on is all that is intended. In contrast, 
suggests that we also mean that 
.
I’ll end by noting that big- notation has some rather distant cousins for which this notation is particularly important. For example, there is the notation, where one writes 
to mean… something. In fact, out of context, it is often entirely unclear what this notation means. This might mean that 
for some constant , or it might mean 
for some constant , or it might mean that both things are true. (Note that including the constant in two places is a convenient trick to avoid needing two constants.) Of course, often the context makes this clear. But, one can be unambiguous by instead writing 
, 
and 
respectively. Other examples of distant cousins include 
, 
, 
, etc. For example, one traditionally writes 
to mean that 
, i.e., that is a negligible function. Hopefully it is clear to the reader what I propose: we should write 
.
![\[f(C) := \int_{-\infty}^\infty e^{-Cx^2} {\rm d} x\]](http://www.solipsistslog.com/wp-content/ql-cache/quicklatex.com-096cdf537e620c218a57694e9aca2bf4_l3.png "Rendered by QuickLaTeX.com")
is proportional to 
. But, what is the constant of proportionality? It’s actually nicer to ask a slightly different question: what is the unique value of 
. A quick numerical computation shows that 
. E.g., here’s some Mathematica code to find this value:
.
is so important for this blog post that it is worth giving it a name. So, I looked through the Greek alphabet for a nice letter that doesn’t get used much and chose the obscure lowercase letter 
—spelled pi in English, and pronounced like “pie”. In other words, by definition 
. (If this implicit definition bothers you, we can equivalently just define 
. But, I find the implicit definition to be more elegant.)
to obtain ![\[1 = 2\int_{0}^{\infty} e^{-\pi x^2}{\rm d} x = \pi^{-1/2} \int_0^{\infty} e^{-u}/u^{1/2} {\rm d} u\; .\]](http://www.solipsistslog.com/wp-content/ql-cache/quicklatex.com-f10d9cf7ba99c79b8b6410cfbffbcb0d_l3.png "Rendered by QuickLaTeX.com")
![\[\pi =\Big( \int_0^\infty e^{-u}/u^{1/2} {\rm d} u\Big)^2\; ,\]](http://www.solipsistslog.com/wp-content/ql-cache/quicklatex.com-a70346615d75d7bd8aad3e871d66f99c_l3.png "Rendered by QuickLaTeX.com")
, i.e., 
. (Recalling that 
for integer 
is “the factorial of 
.”)
given by the probability density function ![\[\Pr[\mathbf{x}] = e^{-\pi \|\mathbf{x}\|^2}\; .\]](http://www.solipsistslog.com/wp-content/ql-cache/quicklatex.com-cbeee2e0bc6e4a6f5288818cb4aa2a7a_l3.png "Rendered by QuickLaTeX.com")
![\[\int_{\mathbb{R}^n}e^{-\pi \|\mathbf{x}\|^2} {\rm d} \mathbf{x} = \int_{-\infty}^{\infty} \cdots \int_{-\infty}^{\infty} e^{-\pi x_1^2 -\cdots - \pi x_n^2} {\rm d}x_1 \ldots {\rm d} x_n = 1\; ,\]](http://www.solipsistslog.com/wp-content/ql-cache/quicklatex.com-8c88f8ef8350b5bf5e3924147dbed5de_l3.png "Rendered by QuickLaTeX.com")
![\Pr[\mathbf{x}]](http://www.solipsistslog.com/wp-content/ql-cache/quicklatex.com-17a91f072153c1ba54d02a280dccc979_l3.png "Rendered by QuickLaTeX.com")
can be written both as a function only of the norm of 
, ![\Pr[\mathbf{x}] = f^*(\|\mathbf{x}\|)](http://www.solipsistslog.com/wp-content/ql-cache/quicklatex.com-2c1674e9adcb304d86d51e6e3e89bd93_l3.png "Rendered by QuickLaTeX.com")
for some continuous function 
, and as a product of functions of its coordinates, ![\Pr[\mathbf{x}] = f_1(x_1)\cdots f_n(x_n)](http://www.solipsistslog.com/wp-content/ql-cache/quicklatex.com-724a32e8712eb42c68f40510a4461d33_l3.png "Rendered by QuickLaTeX.com")
. This makes the Gaussian a uniquely powerful tool for reducing complicated multi-dimensional problems to one-dimensional problems. 
, so that the radius would be ![\[1 = \int_{\mathbb{R}^2} e^{-\pi \|x\|^2} {\rm d} x = \int_0^\infty e^{-\pi r^2} \sigma_r {\rm d} r= \sigma_1 \int_0^\infty e^{-\pi r^2} r {\rm d} r\;,\]](http://www.solipsistslog.com/wp-content/ql-cache/quicklatex.com-7d71e3575dad757294955cdf449254fa_l3.png "Rendered by QuickLaTeX.com")
is the circumference of a circle of with radius 
. (The only facts that we have used here are our definition of 
.) Fortunately, the last integral is easy to compute as ![\[\int_0^\infty e^{-\pi r^2} r {\rm d} r = \frac{1}{2\pi} \cdot \int_0^\infty e^{-u} {\rm d} u = \frac{1}{2\pi} \;.\]](http://www.solipsistslog.com/wp-content/ql-cache/quicklatex.com-f7b0b0433407f63b0c9f6682c331ab63_l3.png "Rendered by QuickLaTeX.com")
!
? This same one neat trick is just as useful in higher dimensions. E.g., what is the surface area 
of a unit sphere in 
because it as an 
-dimensional object that happens to be embedded in 
for its surface area.) Well, we have ![\[1 = \int_{-\mathbb{R}^n} e^{-\pi \|x\|^2} {\rm d} x = \int_0^\infty e^{-\pi r^2} \sigma^{(n-1)}_r {\rm d} r= \sigma^{(n-1)}_1 \int_0^\infty e^{-\pi r^2} r^{n-1} {\rm d} r\; .\]](http://www.solipsistslog.com/wp-content/ql-cache/quicklatex.com-f260e2a2d6410051fb74cc87df3c7792_l3.png "Rendered by QuickLaTeX.com")
.) This integral is a bit less pretty, but using the same approach, we see that ![\[\int_0^\infty e^{-\pi r^2} r^{n-1} {\rm d} r = \frac{1}{2\pi^{n/2}} \cdot \int_0^{\infty} e^{-u} u^{n/2-1} {\rm d} u = \frac{\Gamma(n/2)}{2\pi^{n/2}}\; ,\]](http://www.solipsistslog.com/wp-content/ql-cache/quicklatex.com-65c828363c086f1b820b730be79a4c39_l3.png "Rendered by QuickLaTeX.com")
.
, 
, while 
. (Both of these identities follow from the relation 
, which follows from integration by parts, together with the values 
and 
.) ![\[\sigma_1^{(n-1)} = \begin{cases}\pi^{n/2} \cdot \frac{2}{(n/2-1)!} &n\text{ even}\\\pi^{(n-1)/2} \cdot \frac{2^n \cdot ((n-1)/2)!}{(n-1)!} &n\text{ odd}.\end{cases}\]](http://www.solipsistslog.com/wp-content/ql-cache/quicklatex.com-7093395acfb9701717087f97c5b73145_l3.png "Rendered by QuickLaTeX.com")
as 
. (I.e., “
.
and 
. Plugging in, one sees that the circumference of a circle with radius one is 
(which, ok, we already saw before), and that the surface area of a sphere with radius one is 
. But, we can easily go farther: the surface area in four dimensions is 
, and in five dimensions, it is 
.![\[V^{(n)} = \int_0^{1}\sigma_r^{(n)} {\rm} d r = \sigma_1^{(n)} \cdot \int_0^{1} r^{n-1} {\rm d} r = \sigma_1^{(n)}/n \; .\]](http://www.solipsistslog.com/wp-content/ql-cache/quicklatex.com-08b8932dcb424209e24a111106e869b2_l3.png "Rendered by QuickLaTeX.com")
